|
Lagrangian Particle Code for The Simulation of 2D/3D Fluid Dynamics
|
|
Lagrangian Particle Code for The Simulation of 2D/3D Fluid Dynamics
|
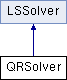
A class which solves the least squares problem by the QR decomposition method. More...
#include <ls_solver.h>
Public Member Functions | |
| QRSolver (std::size_t numRow, std::size_t numCol, double *A, double limitR=1e-3) | |
| Constructor. More... | |
| virtual int | solve (double *result, double *b) |
| returns 0 if success and result will be non-empty returns k<0 if the kth argument is illegal, result is empty returns k>0, k=rank in this case, result is empty More... | |
 Public Member Functions inherited from LSSolver Public Member Functions inherited from LSSolver | |
| virtual | ~LSSolver () |
| Destructor. More... | |
Additional Inherited Members | |
 Protected Attributes inherited from LSSolver Protected Attributes inherited from LSSolver | |
| std::size_t | m_iNumRow |
| The number of rows in matrix A. | |
| std::size_t | m_iNumCol |
| The number of columns in matrix A. | |
| double * | m_vA |
| The matrix A. | |
| double * | m_vb |
| The vector b (the right-hand-side) | |
A class which solves the least squares problem by the QR decomposition method.
Co-author: Yu, Kwangmin (yukwangmin@gmail.com) on initial interface design
Created on: 2014/09/20
|
inline |
Constructor.
Set up the matrix A and other scalar parameters of this class
| [in] | numRow | The number of rows in matrix A |
| [in] | numCol | The number of columns in matrix A |
| [in] | A | The matrix A |
| [in] | limitR | A specified scalar multiplier (<1) for trimming diagonal entry of R in the QR decomposition |
|
virtual |
returns 0 if success and result will be non-empty returns k<0 if the kth argument is illegal, result is empty returns k>0, k=rank in this case, result is empty
Solves the least squares problem Ax = b by the QR decomposition method
A is a mxn matrix, b is a mx1 vector, and x is the solution which is a nx1 vector This method solves for 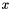 by the following steps:
by the following steps:
![\[ QRPx = b \]](form_3.png)
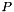 is a permutation matrix
is a permutation matrix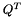 to get
to get
![\[ RPx = Q^T b \]](form_6.png)
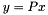
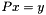 for
for 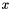
| [out] | result | The x in Ax = b, which is a nx1 vector |
| [in] | b | The right-hand-size, which is a mx1 vector |
Implements LSSolver.
 1.8.6
1.8.6